1. 引言
电子具有电荷和自旋两个维度,由于量子尺寸效应的限制,人们对电子电荷这一维度的应用已经接近极限,但对电子自旋这一维度的应用相对较少。巨磁阻效应(gmr)、隧道磁电阻效应(tmr)以及磁性随机存储器(mram)的发现和应用极大的推动了自旋电子学的发展,自旋电子学作为一门新兴的交叉学科是研究热、磁与自旋相互作用的新兴领域。自旋流是以自旋形式而不是以电子电荷的形式传递信息在信息输运方面有着非常重要的意义。相比于传统电子器件,由于不存在电荷的积聚,避免了因集成度而导致的局部温度过高现象。自旋电子学器件还具有数据处理快、能耗低和非易失性等特点,自旋电子学的研究和应用具有广泛的前景。
研究和应用自旋电子学器件离不开对自旋流的研究,自旋流的产生、调控和探测是自旋电子学研究领域的核心问题。目前产生自旋流的方式主要有自旋泵浦效应(spin pumping effect)、自旋霍尔效应(spin hall effect)和自旋塞贝克效应(spin seebeck effect) [1] [2] [3],分别是利用微波、电流和热流来产生驱动自旋流。本文我们研究的焦点在自旋塞贝克效应(sse),自旋塞贝克效应是近十年来研究的热点之一,其主要原因在于其在自旋电子器件、废热回收利用以及能源节约中的潜在革命性应用。sse是k. uchida等人首次在ni81fe19/pt双层膜中观测到,随后c. m. jaworski在铁磁半导体gamnas中,k. uchida在铁磁绝缘体钇铁石榴石y3fe5o12 (yig) [3] [4] [5] 中均观测到自旋塞贝克效应。近几年,在反铁磁材料nio、α-fe2o3、irmn等反铁磁材料中也观测到sse,这说明sse广泛的存在于各种材料中 [6] [7] [8] [9] [10]。虽然sse最早发现于铁磁金属中,但是对这一效应的研究主要集中在yig/pt双层结构中,主要的原因是yig的阻尼非常低,自旋流在yig中传播距离远,并且没有平面能斯特效应(pne)和反常能斯特效应(ane)等其他杂散效应的污染。
本文主要从以下几个部分来描述自旋塞贝克效应在yig/pt异质结的研究进展。在第一部分,介绍了铁磁金属和铁磁绝缘体中两种不同的自旋流。在第二部分介绍了自旋霍尔效应、逆自旋霍尔效应、异常能斯特效应和自旋塞贝克效应。在第三部分从两个方面总结了自旋流在yig/pt异质结中产生和传播的理论研究进展,一方面是最先提出的磁振子模型;另一方面,从磁振子–声子间的相互作用的角度来解释自旋流在yig/pt异质结中产生和传播。在第四部分,介绍了对yig/pt异质结界面的修饰对自旋流输运的影响。最后一部分对文章进行总结和对yig/pt异质结中自旋流的研究进行展望。
2. 自旋流
电子是带负电荷的基本粒子,它决定着凝聚态物质的各种性质。除了电荷,电子还有自旋属性。自旋是磁性的主要来源,因此,当固体中一定量的电子自旋朝向一个确定的方向时,这个固体就变成了磁性材料。正如我们所知,电子电荷的定向流动形成电荷流。由于电子携带着电荷和自旋,电荷流的存在自然意味着自旋流的存在,这种流动被称为自旋流。下面介绍两种不同的自旋流。
在铁磁金属中,自旋流由传导电子携带。若用
和
分别表示自旋向上和自旋向下电子的电荷流密度,则总的电荷流密度为
。类似的自旋流密度为
,
为约化普朗克常数 [11] [12]。
如图1(a)所示,当等量的自旋向上和自旋向下的电子向相同的方向移动时,总的
恒定不变而
,这种情况下没有角动量的传递。图1(b)中当等量的自旋向上和自旋向下的电子向相反的方向移动时,总的
恒定不变而
,这样仅有角动量的传递而没有电荷流。
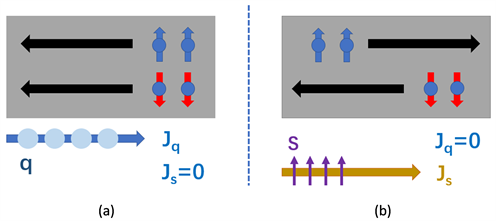
. (a) an illustration of a pure charge current, the same number of spin-up and spin-down electrons move in the same direction. this leads to a net charge current density
,while the spin current density
vanishes. (b) an illustration of a pure spin current, the same number of spin-up and spin-down electrons move in the opposite direction. this leads to a net spin current density
, while the charge current density
vanishes
图1. (a) 纯电荷流的示意图,等量的自旋向上的电子和自旋向下的电子朝着相同的方向运动。这导致存在一个净电荷流密度
,而自旋流密度
消失。(b) 纯自旋流的示意图,等量的自旋向上的电子和自旋向下的电子朝着相同的方向运动。这导致存在一个净自旋流密度
,而电荷流密度
消失
铁磁绝缘体中不存在传导电子,自旋流可以通过激发自旋波或磁振子以非平衡的方式驱动。自旋波是磁有序态的一种集体激发。给铁磁绝缘体施加一个外磁场h,当磁矩与h平行排列时,能量最小。若原子的磁矩如果与h不在一个方向上,自旋在磁场h周围将会不断地进动。自旋通过交换作用与最近邻自旋耦合,如果其中一个自旋相对于基态方向倾斜,邻近的自旋倾向于这种倾斜,整个系统将开始做集体运动,这样就行成了自旋波,图2(a)和图2(b)分别是一维原子链自旋波的侧视图和俯视图 [13] [14] [15]。
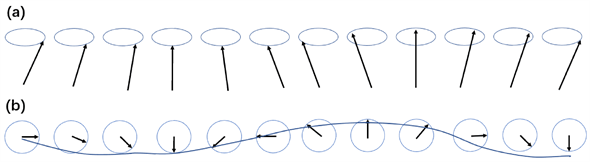
. spin wave of a one-atomic chain in (a) side view and (b) top view
图2. (a) 一维原子链自旋波侧视图 (b) 一维原子链自旋波俯视图
3. 自旋塞贝克效应及其相关效应
3.1. 自旋霍尔效应与逆自旋霍尔效应
d’yakonov和perel于1971年首次预测了自旋霍尔效应(she)的存在,she指的是横向于外加电场的纯自旋流的产生,该电场导致系统中伴随的自旋不平衡 [16]。针对she提出了两种不同的机制:一种是由于自旋向上和自旋向下电子散射的不对称性。另一个是由于拓扑能带结构,这是内在sse机制,最终源于电子运动或自旋轨道相互作用的相对论效应 [17] [18] [19]。如图3(a),在she中,电荷流产生自旋流的大小为:
(1)
在这里
表示自旋流密度,
表示电荷流密度,
表示自旋方向,
表示自旋霍尔角,是材料的内禀属性,它反映了自旋相关散射效应的大小。逆自旋霍尔效应(ishe)是she的逆效应 [20],如图3(b),在具有自旋轨道耦合的材料中自旋流转化为电荷流,所产生电荷流的大小为:
(2)

. (a) the spin hall effect converts the charge current density
into a pure spin current density
with a spin direction of
. (b) the inverse spin hall effect converts the pure spin current density
with the spin direction
into the charge current density
图3. (a) 自旋霍尔效应将电荷电流密度
转换为自旋方向为
的纯自旋流密度
。(b) 逆自旋霍尔效应将具有自旋方向
的纯自旋流密度
转化为电荷电流密度
3.2. 自旋塞贝克效应
塞贝克效应是指将导体放置于温度梯度中将产生电压。其效率由塞贝克系数s表示,该系数定义为产生的电压与温差的比值,并由散射率和传导电子的密度决定 [21]。自旋塞贝克效应指的是在铁磁性材料中可以通过施加温度梯度产生自旋流,当探测层与磁性材料相接触时,sse将诱导自旋流注入到探测层中,由于探测层中的自旋轨道相互作用,sse诱导的自旋流将通过逆自旋霍尔效应转换为可测量的sse电压,如图4(a) [22]。类似于塞贝克系数的定义,自旋塞贝克系数定义为:
(3)
这里
为自旋塞贝克系数,v是ishe所测电压,
表示温度梯度。
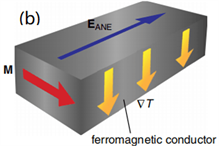
. (a) longitudinal spin seebeck effect and inverse spin-hall effect,
、∇t、h、m and
denote the electric fields, temperature gradient, magnetic field, magnetization vector, and spatial direction of the thermally generated spin current, respectively. (b) schematic illustrations of the anomalous nernst effect [22]
图4. (a) 纵向自旋塞贝克效应和逆自旋霍尔效应,
、∇t、h、m和
分别表示热产生的自旋流的电场、温度梯度、磁场、磁化矢量和自旋流。(b) 异常能斯特效应示意图 [22]
探测sse主要有两种实验装置,分别是横向自旋塞贝克(tsse)装置和纵向自旋塞贝克(lsse)装置 [1] [2] [3] [22]。如图5(b)所示,在tsse装置中温度梯度与自旋流方向相互垂直,sse最早就是在这一结构中发现的,但是在横向加温装置中,由于所测样品与衬底的热导不同就会存在一个纵向的温度梯度 [23]。目前在sse实验中主流的实验装置是纵向装置,如图5(a)所示。lsse结构更为简单,在纵向加温结构中温度梯度与自旋流方向平行。
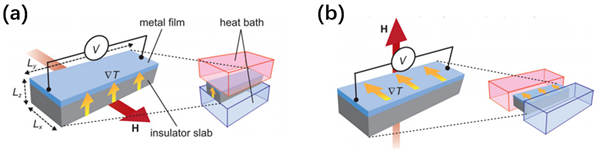
. (a) schematic illustrations of the longitudinal heating device for spin seebeck effect. (b) schematic illustrations of the transverse heating device for spin seebeck effect [22]
图5. (a) 自旋塞贝克效应纵向加温装置示意图。(b) 自旋塞贝克效应横向加温装置示意图 [22]
如图4(b)所示,由于反常能斯特效应(ane)与纵向自旋塞贝克效应与有相同的结构类型,在观测sse电压信号时不可避免的要受到ane信号的污染,将自旋塞贝克效应从反常能斯特效应中分离也是当今研究的热点 [24] [25]。在纵向nife/pt结构中插入nio层排除了nife中异常能斯特效应以及pt中磁近邻效应的污染 [26]。多方面的研究也表明yig中ane对所测sse电压的影响可以忽略不计 [27] [28] [29]。
4. yig/pt异质结中sse产生与输运自旋流理论研究
4.1. 磁振子模型
4.1.1. 自旋流产生于fmi/nm界面
2010年,j. xiao等首次在磁性绝缘体yig中观测到sse,证明了传导电子的存在并非产生sse的必要条件 [5]。j. xiao首次使用散射理论提出了磁振子驱动sse模型 [30]。如图6所示。由于铁磁层(fm)层中的磁振子与非磁层(nm)层的传导电子对温度有不同的热响应,由波动耗散定理可知,fm层中有效磁振子温度
与nm层中有效传导电子温度
的不同引起了fm层的磁化热波动和nm层的热噪声 [31]。fm层的磁化热波动驱动自旋泵浦流从fm层流向nm层,这一自旋泵浦流正比于
。由于nm层热噪声的存在,自旋流由nm层流向fm层形成自旋回流,自旋回流的大小正比于nm层中有效传导电子温度
。注入自旋流的大小为:
(4)
. spin pumping current isp and fluctuating spin current ifl in sse [30]
图6. sse中自旋泵浦流与自旋回流示意图 [30]
在这里
是磁振子扩散长度,
是自旋混合电导,
是玻尔兹曼常数,
是磁相干体积.自旋流的大小依赖于fm层中有效磁振子温度
与nm层中有效传导电子温度
。
h. adachi在铁磁绝缘体中使用线性响应理论完善了这一模型,并提出了局域自旋注入与非局域自旋注入,如图7所示 [32]。局域自旋注入过程为p1,假设
、
和
之间并无热量交换,
层与
层的温差驱动热磁振子局域注入。注入的自旋流大小为:
(5)
表示局域自旋数、
表示fm/nm界面s-d交换耦合、
表示局域自旋大小,
自旋弛豫时间,
是自旋扩散长度,
是顺磁化率。
当
与
温度相同时,由于磁振子传播的平衡条件,自旋流消失,即“局部”过程不能解释yig膜与附接的pt膜之间不存在温差的实验。在非局域自旋注入模型
中,
、
和
之间有热量交换,当磁振子感受铁磁体内部的温度梯度而偏离局部热平衡时,磁振子的非平衡传播将对热自旋注入有贡献 [33]。自旋流的大小为:
(6)
和
分别是相邻两区域温度,自旋流的大小正比于铁磁层中相邻区域的温差。
l. chotorlishvili在j. xiao和h. adachi理论的基础上,提出了自旋流的大小与外加磁场和磁各向异性有关 [34]。自旋流随着磁振子温度的升高而饱和,并且饱和温度随着磁场和磁各向异性的增加而增加。同时证明了线性响应理论仅在很窄的温度范围内有效,外加磁场越小,线性响应理论与实验偏差越大,随着外加磁场的增强,线性响应理论与实验拟合的越好。磁各向异性效应增加了磁场的影响,自旋流随着磁各向异性的增加而达到饱和。
. feynman diagrams expressing the spin current injected from the ferromagnet (fm) to the nonmagnetic metals (nm). the thin solid lines with arrows (bold lines without arrows) represent electron propagators (magnon propagators) [33]
图7. 从铁磁体(fm)到非磁性金属(nm)的自旋流的费曼图。带箭头的细实线(没有箭头的粗线)表示电子传播(磁振子传播) [33]
4.1.2. 自旋流产生于fmi中
另外一种lsse模型,认为在fmi/nm体系中,lsse起源于由温度梯度导致的贯穿于铁磁绝缘体内部的磁振子流,提出了磁振子自旋流产生于薄膜内部而非界面,但需fmi与nm层接触,以保证自旋流的连续性 [35]。fm层的磁振子自旋流为:
(7)
第一部分表示温度梯度对磁振子自旋流的影响,后俩部分是由于磁振子积聚的空间变化引起的。
为磁振子扩散系数,
为磁振子扩散长度,其中
为磁振子–声子作用弛豫时间。a和b由
fmi/pm结构的边界条件决定。fmi/pm界面的磁振子自旋流密度为:
(8)
f与材料自身的性能相关,
是与f层厚度相关的因素,
为有效自旋混合电导。
(n = 0、1、2、s)与波数和磁振子弛豫时间相关。这一公式可以解释sse与fmi层的厚度依赖关系和温度依赖关系。
在高磁场下,通过研究在pt/yig双层膜结构中lsse温度与厚度的依赖关系,在实验上对磁振子模型有了更细致的认识,如图8(a)和图8(b)所示 [36]。在300 k~5 k温度范围内施加高磁场抑制lsse信号,随着pt/yig结构的温度降低,这种抑制作用增强,并且在同一温度下,yig越厚,所测得的sse电压信号越大,表明低频磁振子对lsse提供一个主要的贡献,而非高频磁振子。lsse信号及其磁场依赖性受yig薄膜厚度的影响,低频率的磁振子具有较长的能量弛豫长度,sse的热自旋转换效率与磁振子的频率有着紧密的联系。
4.2. 磁振子–声子相互作用
针对铁磁绝缘体中sse的产生机制,已经提出了几种磁振子模型,但这几种磁振子模型在解释sse的产生机制的细节上还有争议。正如我们所知,声子负责大多数固体中的热传导,在磁性材料中,磁振子(自旋的集体激发)也参与自旋和热的输运。磁振子和声子是固体中两个最基本准粒子,并且可以结合在一起形成混合准粒子,现在铁磁绝缘体中sse的产生机制的研究焦点在磁振子–声子耦合 [37] [38] [39]。最近研究表明,铁磁体对弹性波的共振吸收也可以驱动自旋电流,这种方法被称为声学自旋泵浦(asp),声学泵浦是sse的共振等价物 [40]。asp的基本机制是通过磁弹性效应将弹性波(声子)和自旋波(磁子)的耦合,磁振子自旋泵浦有望为基本理解磁振子–声子耦合在自旋电子和磁振子现象中的作用提供必要的信息。
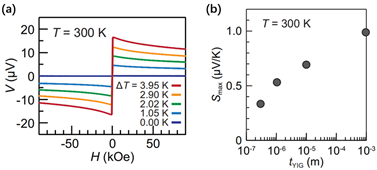
. (a) h dependence of v in the pt/yig-slab sample at t = 300 k for various values of
. (b)
dependence of
at t = 300 k [36]
图8. (a) t = 300 k时pt/yig 样品中v对不同t的h依赖性. (b) t = 300 k时
对
的依赖关系 [36]
4.2.1
. 直接探测磁振子–声子温度差异
理解铁磁绝缘体sse产生机制的一个关键就是理解自旋–晶格的相互作用,即磁振子–声子之间的耦合。磁振子是材料磁性结构激发的量子化,声子是晶格振动的量子化。最初在横向pt/yig结构中,sse的产生机制被认为铁磁绝缘体中磁振子和声子在横向温度梯度下存在温差。m. agrawal采用布里渊光散射(bls)光谱法检测用于检测高度空间局域化的热交换磁子,测量磁振子的温度
,同时将红外(ir)相机垂直于胶片表面,同时测量声子温度
的空间分布,探测结构和红外图像如图9(a)和图9(b)所示 [41]。
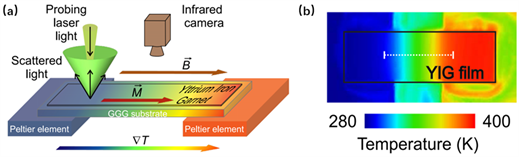
. (a) two peltier elements are placed at both ends of yig/ggg to produce a transverse temperature gradient. the temperature of the magneto is measured by bls, and the thermal image of the system is obtained by infrared camera. (b) infrared image of the yig film shown in (a) [41]
图9. (a) 两个帕尔贴模块放在yig/ggg两端产生一个横向的温度梯度,bls来测量磁振子的温度,使用红外摄像机获得系统的热图像。(b) (a)中yig薄膜的红外图像 [41]
测量结果表明,声子温度沿yig条带长度方向分布是均匀的,随着yig薄膜温度的升高,磁振子频率单调下降,这是由于热磁振子分布的增加降低了系统的磁化强度。虽然磁振子频率的单调下降不能通过将磁化作为唯一的温度相关量来衡量,但主要的贡献来自磁化。局域磁振子频率可以表示为磁振子温度
的函数。声子温度
和磁振子温度
由后向散射磁振子(bsm)模式测量频率的三阶多项式拟合计算,绘制为沿yig膜的位置的函数。
和
之间的最大差异仅为
的2.8%,与理论预期相反 [42]。
人们普遍的将自旋塞贝克效应的产生归因于磁系统中磁振子和声子在横向温度梯度下存在温差,这一测量结果表明没有这种差异。另一种合理的解释是磁振子温度与波数有关
,并在磁振子光谱的较长波长的区域可以建立能够产生自旋塞贝克效应的
和
之间的差异 [43]。这表明,与先前的认识相反,分布在磁振子光谱长波范围内的磁振子引起了sse中磁振子与声子温度之间不平衡。
4.2.2
. 声子—磁振子共振条件
p. a. deymier等人研究了具有两种磁弹性耦合形式的铁磁体的经典一维离散模型,揭示了声子和磁振子共振的条件 [44]。并且在多尺度微扰理论的框架下,分析了自旋自由度分量中耦合限制为对角项的情况下的非线性声子–磁振子相互作用。在这种情况下,一个声子与两个磁振子共振是泵浦的主要机制。耦合对色散关系的影响取决于声子和磁振子激发的振幅的平方。当磁振子和声子有非线性相互作用时,磁振子和声子的频率分别为:
(9)
(10)
在这里
和
是没有相互作用时,磁振子和声子的频率。
代表
,
和
分别代表磁振子
和声子的振幅,p(k)和q(k)分别是波数的函数,表示为:
(11)
(12)
无量纲量
,k是一个正的常量,
是自旋磁矩沿着z方向的零级近似。
在磁弹性耦合被限制为自旋分量中的非对角项的情况下,对线性声子–磁振子相互作用的直接分析表明,单声子–单磁振子共振作为泵浦机制。磁弹性耦合在这种情况下声子和磁振子的色散关系的影响与波的振幅无关。当
时,线性耦合的声子和磁振子的频率为:
(13)
在这里
,
是正的常数。还研究了外部磁场对线性共振条件的影响,线性系统关于磁场强度的行为类似于非线性系统的行为。外加磁场在弹性波固定频率下的强度变化可以用来调谐系统向共振方向运动,外加磁场在共振时的强度随着声波频率的增加而增加 [44]。
4.2.3
. 磁振子极化子
磁振子和声子之间的耦合来源于磁性晶体中的自旋轨道相互作用、偶极–偶极相互作用和交换相互作用 [45]。这种耦合的强度在未耦合的磁振子和声子色散的交点附近达到最大。在交点区域,系统的标准模式不再是单纯的有磁性的或者弹性的,而是这两种的混合物。这种耦合导致混合磁振子和声子模式的形成,称为磁振子极化子 [46] [47]。
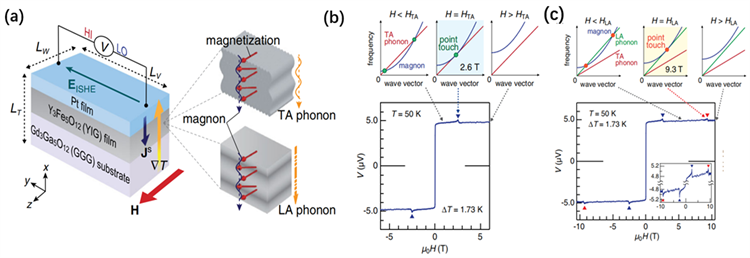
takashi kikkawa在如图10(a)所示的pt/yig/ggg结构中观测到了低温下所测电压信号出现了异常峰,通过磁振子–声子相互作用很好的解释了实验结果 [48]。当磁场增强时,由于塞曼相互作用,磁振子色散向高频移动而声子的不会。在图10(b)中可以看到,当
,磁振子色散曲线与ta-声子色散曲线相交两次,当
,磁振子色散曲线与ta-声子色散曲线相切,当
,磁振子色散曲线与ta-声子色散曲线没有接触在
处,出现一个异常峰。同样在图10(c)也可以看到在
处也出现异常峰。由此可以知道磁振子–声子的耦合作用增强sse的电压信号,若用i (i = 0, 1, 2)表示磁振子色散曲线与ta(la)声子色散曲线交点,则测得的电压信号
。
. (a) the longitudinal sse in the pt/yig/ggg sample, the close-up of the upper (lower) right shows a schematic illustration of a propagating magnon and ta (la) phonon. (b) magnon and ta-phonon dispersion relations for yig when
,
,
.
of the pt/yig/ggg sample for δt = 1.73 k at t = 50 k for
. (c) magnon, ta-phonon, and la-phonon dispersion relations for yig when
,
,
.
of the pt/yig/ggg sample for δt = 1.73 k at t = 50 k for
[48]
图10. (a) 纵向sse中,pt/yig/ggg结构示意图,右上方(下方)显示了磁振子和ta(la)声子的传播示意图。(b) 在yig中,磁振子和声子的色散关系在
,
,
及对于
,在t = 50 k,δt = 1.73 kpt/yig/ggg样品的
与v(h)的关系。(c) 磁振子,ta声子,la声子色散关系在
,
,
及对于
,在t = 50 k,δt = 1.73 kpt/yig/ggg样品的
与v(h)的关系 [48]
对于自旋塞贝克系数s,hta和hla处的两个峰有不同的温度依赖性,hta处的峰随着温度的降低明显增强,在t < 10 k时,hla处的峰随着在温度的降低逐渐减小。这是因为在
和
分支的交叉点有不同的能量量级。在磁振子-la声子交点附近具有能量的磁振子的激发被迅速抑制,导致hla最低t处的s峰消失。因此,sse可以被探测到不仅仅是磁振子动力学,还涉及到声子动力学 [44] [49]。
5. 提高yig/pt界面自旋混合传导
纯自旋流具有传递自旋角动量而无净电荷流的独特特性,因此具有更高的能量效率。然而,sse器件的热电转换性能在实际应用中仍然不理想,热电转换效率提高的研究经久不衰。自旋塞贝克效应所产生电压大小由以下因素决定 [30]:
(14)
在这里
与磁振子-声子温差成正比,
是自旋霍尔角,
是电阻率,
是自旋混合传导,
是旋磁比,e是电子电荷,
是玻尔兹曼常数,l是探测点之间的距离,
是饱和磁化强度,
是磁相干体积,a是铁磁氧化物层与非磁金属层界面之间的接触面积。
决定自旋塞贝克效应的一个重要参量就是铁磁氧化物和非磁金属界面之间的自旋混合传导 [50] [51]。在这里我们分别列举在pt/yig结构中插入金属、半导体和反铁磁材料来提高pt/yig异质结的自旋混合传导和改善界面质量,从而增强自旋塞贝克效应。
5.1. 在pt/yig中插入薄fe层
y. iwasaki等测试了
和
对插入fe层厚度依赖关系,发现当0.3 nm厚的fe插入pt/bi:yig层中时,热电转换效率达到峰值,如图11(a)所示 [52]。而
可以通过以下公式进行计算:
(15)
ms、γ、df、g、μb和w分别是饱和磁化强度、旋磁比、bi:yig的层的厚度、g因子、玻尔磁子和微波的角频率。
和
分别是pt/fe/bi:yig/sggg和bi:yig/sggg的fmr光谱宽度δh。图11(b)显示了铁磁共振fmr的光谱,同时平面内外磁场h的大小发生了变化,微波频率固定在
。bi:yig/sggg显示了最窄的fmr光谱宽度w,如图11(b)的插图所示。在bi:yig层上沉积铂层时,fmr光谱宽度增大,当插入0.3 nm fe层后,fmr光谱宽度进一步增大。通过将这些测量的宽度代入方程(15),可以得到
。进一步说明了通过插入几个原子层厚的铁磁层可以提高自旋混合传导,从而提高自旋流的注入效率。
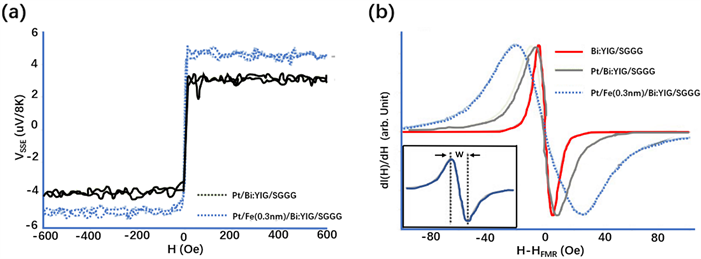
. (a) fine dotted lines and thick dotted lines represent the size of vsse measured in pt/bi:yig/sgg and pt/fe (0.3 nm)/bi:yig/sgg structures, respectively. (b) fmr spectra of bi:yig/sggg, pt/bi:yig/sgg pt/fe (0.3 nm)/bi:yig/sggg in plane and in-plane magnetic fields [52]
图11. (a) 细虚线和粗虚线分别代表pt/bi:yig/sggg和pt/fe(0.3 nm)/bi:yig/sggg结构中所测的vsse的大小。(b) 平面内外磁场bi:yig/sggg、pt/bi:yig/sggg和pt/fe(0.3 nm)/bi:yig/sggg的fmr光谱 [52]
5.2. 在pt/yig中插入薄ni80fe20层
nife是一种典型的铁磁性金属,每个原子都有一个磁矩沿同一方向排列,0.355 nm的面心立方nife磁矩密度为18 μb/nm2。hiromi yuasa等在yig(1 mm)/pt(5 nm)界面中间插入0.6 nm厚ni80fe20薄层,如图12(a)所示。比较bulk-yig/pt (5 nm)与bulk-yig/nife (0.6 nm)/pt(5 nm)的v-h曲线可知,在δt = 13 k和δt = 18 k下,插入0.6 nm的ni80fe20薄层之后,自旋塞贝克电压都提高了2.1倍,如图12(b)和图12(c)所示 [53]。
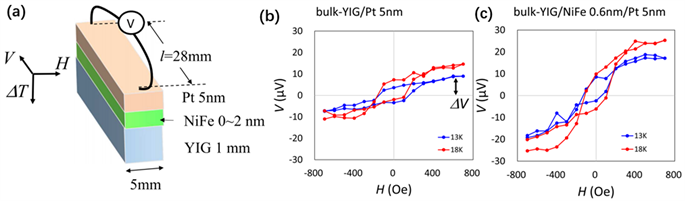
. (a) schematic image of sample structure and measurement configuration. (b) generated voltage v dependence on a magnetic field h for bulk yig/pt 5 nm and bulk yig/nife 0.6 nm/pt 5 nm when δt was 13 k and 18 k [53]
图12. (a) 样品结构及测量装置示意图。(b) 在δt = 13 k和δt = 18 k下,bulk-yig/pt (5 nm)和bulk-yig/nife (0.6 nm)/pt(5 nm)的v-h曲线 [53]
图13(a)与图13(b)展示了sse系数s与插入的镍铁合金厚度的关系。一方面nife的插入提高了磁矩密度,提高了磁性与非磁性部分界面处的自旋混合传导。另一方面,随着nife的厚度增加到0.6 nm后,自旋seebeck系数s减小。这是因为金属部分的增厚降低了整个样品电阻,根据欧姆定律,所产生的电压降低,磁矩密度在nife为0.6 nm处达到饱和 [54]。对铁磁绝缘体层与重金属层之间界面上的磁矩密度的控制是提高界面自旋混合传导一个有效的方法,选择合适材料以及合适厚度的铁磁层,对自旋流的输运有着重要的影响。
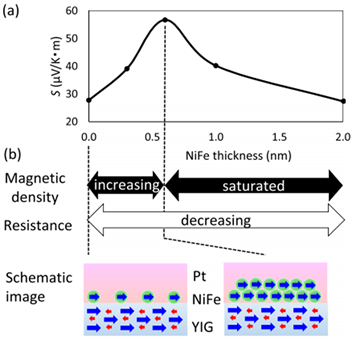
. (a) spin seebeck coefficient s dependence on the inserted nife thickness. (b) behaviors of the magnetic moment density and the resistivity when nife thickness is changed, and schematic illustrations of nife coverage [53]
图13. (a) 自旋塞贝克系数s与插入nife厚度的关系。(b) 改变nife厚度时的磁矩密度和电阻率的变化和nife覆盖范围示意图 [53]
5.3. 在pt/yig中插入薄 层
磁各向异性在确定yig/pt结构中的lsse中起着重要作用。除了体(磁晶)各向异性外, yig表面的垂直磁各向异性(pma)也影响自旋流输运,从而影响lsse行为。由于yig的pma在yig与其它材料相接触时可能发生改变,在绝缘体(yig)和金属(pt)之间沉积c60半导体有望纠正自旋–电导失配问题 [28] [54]。自旋流在c60具有较长的扩散长度,大约为100 nm,有机半导体c60的存在可以改善yig/pt界面的自旋混合传导。
das在yig和pt层中间插入5 nm的c60薄层后,yig/pt的lsse电压由150 nv增加到240 nv [54]。图14(a)和图14(b)分别展示了yig/pt和yig/c60/pt结构在300 k时
的磁场依赖性。c60的存在极大的改善了yig/pt的界面质量,增大了yig/pt界面的自旋混合传导。yig/c60/pt和yig/pt之间的自旋流比为:
(16)
在这里
是自旋流,g是自旋流传导,λ是自旋扩散长度,
是c60层的厚度。
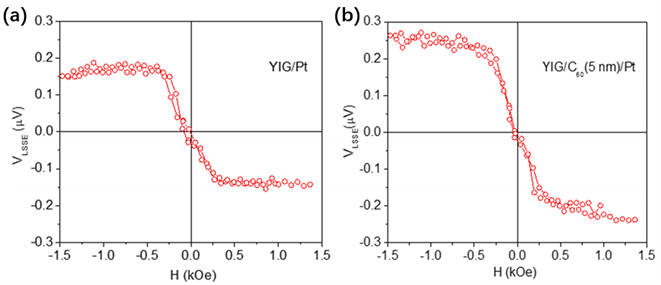
. the magnetic field dependence of lsse voltage taken at 300 k for the temperature gradient of 1 k in the (a) yig/pt and (b) yig/c60/pt systems [54]
图14. (a) yig/pt和(b) yig/c60/pt系统中,当温度梯度为1 k时,在300 k时,lsse电压的磁场依赖性 [54]
5.4. 在pt/yig中插入薄nio层
weiwei lin等报道在nm/yig界面插入nio反铁磁层,sse电压信号有一个巨大的提高,并且在反铁磁层neel温度附近,所测电压信号达到最大值,如图15(a) [55]。在图15(b)和图15(c)中可以看到,由于nio的插入,ta/nio/yig中
的信号有了大幅度提高,但因其ta与pt具有相反的自旋霍尔角,ta/nio/yig中
的信号与pt/nio/yig中的相反。在这两种情况下,nio间隔层的存在隔绝了ane信号,而只保留sse信号,
信号有了极大的提升。同样将coo反铁磁层插入pt/yig层中也可以观察到类似现象 [56]。
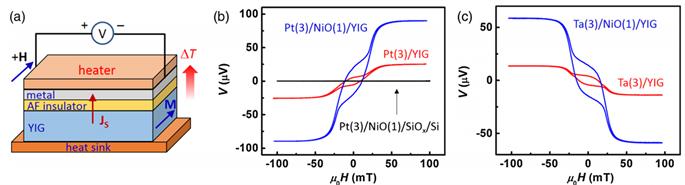
. (a) thermal spin transport measurements. (b) the functions of pt(3 nm)/yig, pt(3 nm)/nio(1 nm)/yig and pt(3 nm)/nio(1 nm)/siox/si inverse spin hall voltage v and applied magnetic field h. the temperature of the metal layer is about 303 k, and the temperature gradient across yig is about 10 k/mm. (c) functions of ta(3 nm)/yig and ta(3 nm)/nio(1 nm)/yig inverse spin hall voltage v and external magnetic field h [55]
图15. (a) 热自旋输运测量示意图。(b) pt(3 nm)/yig、pt(3 nm)/nio(1 nm)/yig和pt(3 nm)/nio(1 nm)/siox/si逆自旋霍尔电压v与外加磁场h的函数。金属层的温度约为303 k,穿过yig的面外温度梯度约为10 k/mm。(c) ta(3 nm)/yig和ta(3 nm)/nio(1 nm)/yig逆自旋霍尔电压v与外加磁场h的函数 [55]
6. 总结与展望
本文从实验研究和理论进展出发,总结了铁磁绝缘体yig中sse产生与作用机制,对磁振子模型和磁振子–声子相互作用模型的研究与发展做出了阐述,并对每种模型的优劣做出了对比。对于磁振子模型,这一理论优势体现在:① 这一理论引入了磁振子对fm/nm界面的热导率的贡献,并且这一理论适用于铁磁性金属和绝缘体,对自旋热电子学有着重要贡献。② 预测了yig的自旋扩散长度在毫米范围内。③ 证明了sse中自旋流只是局域传输,并且提出衬底对所观测到信号的影响。但是这一理论也有明显的不足之处:① 由于磁振子与声子的热响应时间不同,磁振子模型中并不能准确的计算磁振子与声子的温差。② 原则上,磁振子模型对铁磁绝缘体和金属都适用,但是对于铁磁性金属py的计算与实验测量有较大差距。
对于磁振子–声子相互作用这一模型的理论优势体现在:① 证明了横向自旋sse是由磁振子与声子之间的温差引起的。② 揭示声子与磁振子共振的条件,分析了自旋这一自由度分量中对角项耦合的非线性声子–磁振子相互作用。③ 利用这一模型可以确定磁性绝缘体中自旋扩散长度。④ 为利用声子控制自旋流开辟了一条途径。这一理论表明声子动力学对sse有着重要的贡献。但是这一模型仍有不能解释的实验现象和问题:① 声子不具有极性,那么声子是如何携带并传递磁振子的极化信息。② 声子是如何与磁振子相互作用并将极化信息传递给磁振子,③ 对磁振子温度的直接测量也是一个挑战。④ 磁振子–声子相互作用的增强区域主要在高场和低温区域,在这一区域对自旋流的应用也是一个挑战。理论模型的进一步完善,对sse的理解及其应用有着不容忽视的作用。
提高自旋混合传导主要是通过提高界面磁化密度,减少界面的垂直磁各向异性,从而减小界面对自旋流的散射,并提高自旋流的弛豫时间。所以界面材料的选择对自旋混合传导的提高有显著的意义。当前的研究集中在重金属层和铁磁绝缘体之间插入薄金属层,从而大幅度提高界面磁化密度,但是面临两个问题:① 金属层中存在传导电子,可能会产生其它效应污染自旋塞贝克效应;② 自旋流在金属层中的传播长度只有几纳米。所以我们认为界面处材料的选择应该集中在反铁磁绝缘体材料中。插入反铁磁绝缘体来提高自旋混合传导还具有以下优势:① 自旋流的一个重要应用就是计算机磁盘驱动器的读头,这些读取头对磁场的变化很敏感,反铁磁材料中相邻原子的自旋(固有角动量)指向相反的方向,因此材料不易受到外磁场的扰动。② 反铁磁材料,不产生杂散场,显示出超快动力学,这可以使设备在太赫兹尺度(1012赫兹)的频率下运行,并可能产生较大的磁输运效应。③ 实验上已经探测到自旋流在反铁磁材料传播距离可到数10 um的量级,理论上也提出自旋流在理想反铁磁中的传播距离可以达到无限远。
参考文献